Leonhard Euler and Graph Theory

Leonhard Euler was born on April 15th, 1707. He was a Swiss mathematician who made important and influential discoveries in many branches of mathematics, and to whom it is attributed the beginning of graph theory, the backbone behind network science.

A short story about Euler and Graphs

The link between Leonhard Euler and graphs comes from the solution that he presented in 1735 to the problem known as the Seven Bridges of Königsberg. Kóningsberg, a merchant city in the Pregel River, was the capital of Eastern Prussia (now Kaliningrad, Russia). The city had seven bridges connecting, five connecting the island of Kneiphof to the mainland and two crossed the two branches of the river. The arrangement of the bridges gave birth to the following puzzle:

Can one walk across all seven bridges and never cross the same one twice?

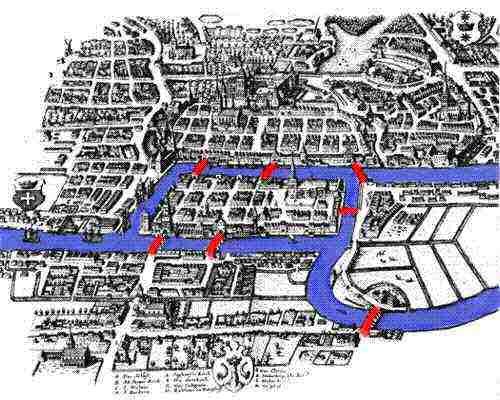
The problem remained unsolved until 1735 when Leonhard Euler presented proof that such a path does not exist. Euler represented each of the land areas with letters A, B, C, and D. Next he connected with lines all pieces of land that had a bridge between them. This abstraction of the problem is a graph, where nodes were pieces of land, and links were the bridges.

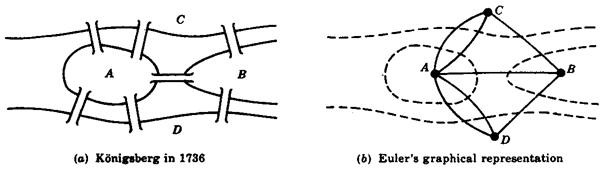
With this abstraction, Euler made an observation: “If there is a path crossing all bridges, but never the same bridge twice, then nodes with an odd number of links must be either the start or endpoint of this path”. And for the Königsberg graph, this was not the case, all of the nodes had an odd number of links, so no such path could satisfy the problem. Euler proof was the first time a mathematical problem was solved using a graph.

Graphs nowadays

Euler’s abstraction is in the root of Network Science, nowadays we use networks to study different complex phenomena, like the spread of epidemics, urban mobility, social systems, economics, and biological systems, among other fields of studies.

The abstraction of a city as a graph help us map the different types of transportation infrastructure into a multiplex network, in which each layer is transportation infrastructure, take for example the above video, in which Manhattan is mapped into a multiplex network, with their pedestrian, bike, subway and street infrastructure. Using this abstraction we can study problems such as how to improve bicycle connectivity, identify underserved areas of a city and their quality of life.