Maximizing bike infrastructure: How to connect a fragmented bicycle network using python

Recently I wrote about how fragment bicycle infrastructure can be (If you din’t get the email, make sure to subscribe here), even Amsterdam has some missing connections in its bicycle network, although not as many as London. Getting to know that the network is not complete is the first step towards having a good bicycle infrastructure network. The next step? Connect it.

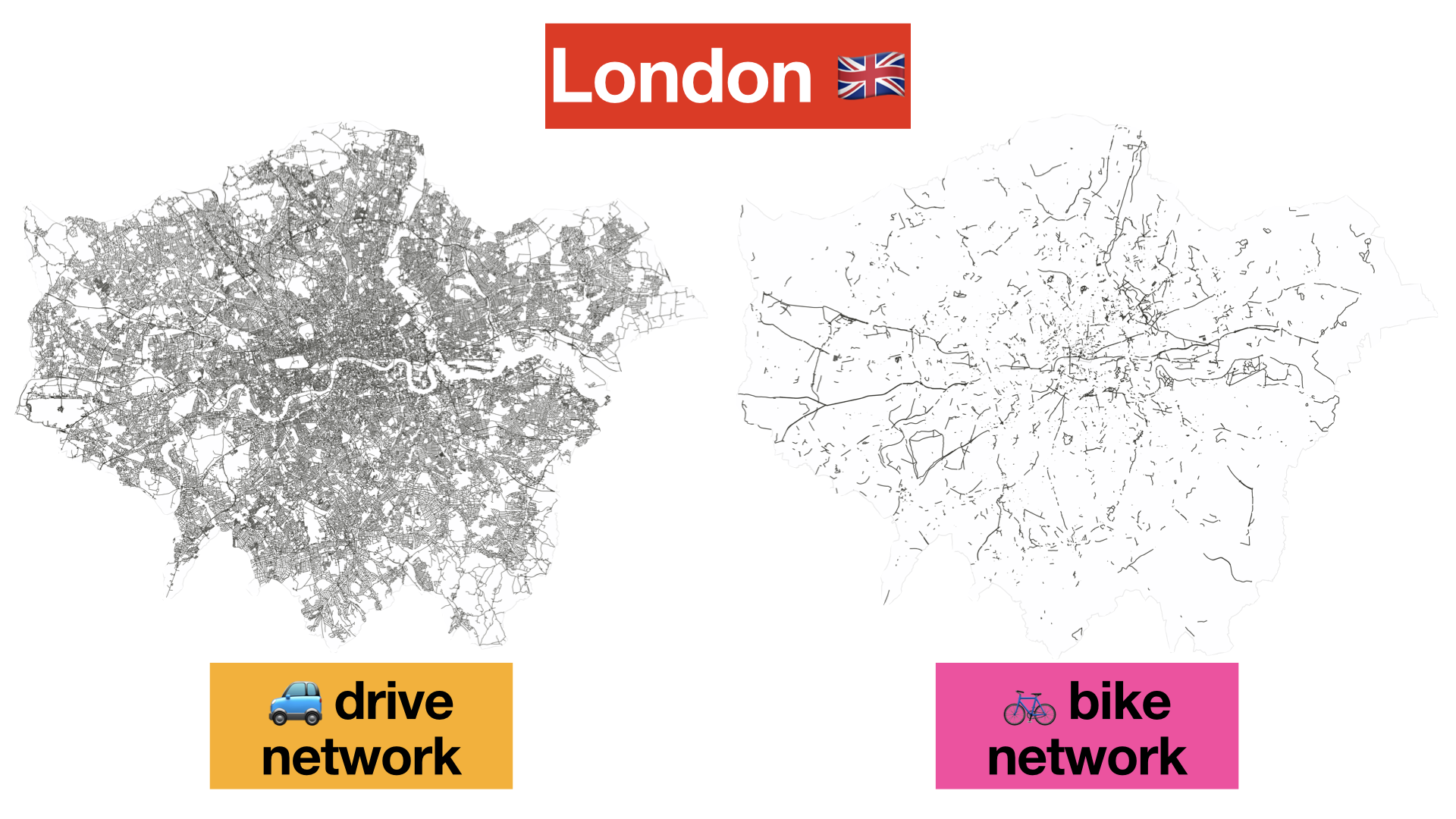Comparison between London’s drive and bike networks. The drive network is consolidated into a single component, while the bike network has more than 3,000 different component. Data from Open Street Map contributors retrieved in 2019.

There are multiple approaches one can follow to connect a broken network, or even to start one from scratch, such as following a grid triangulation, a minimum spanning tree based on seeds along the city, or using the existing bike network to find missing links and connect them.

Most cities that already have some bicycle infrastructure in place can benefit of using an approach that takes the existing network as a seed to improve it. An example of such algorithm is: Using the existing network, find the two largest components, then find the shortest connection between them, and connect them, then repeat this step until everything is connected. This way one minimizes the length of the new connections, while maximizing the gain of new bike lanes.

The algorithm in Python looks as follows:

def largest_to_second(connected_components:list[nx.Graph])->dict[str, Union[int,float]]:
    '''
    Find the closest pair of nodes between two different connected components.
    ---
    connected_components: list connected components

    returns: dict nodes i and j and distance
    '''
    closest_pair: dict[str, Union[int,float]] = {'i': 0, 'j': 0, 'dist': np.inf}
    for i in connected_components[0].nodes(data=True):
        i_coord = (i[1]['y'], i[1]['x'])
        for j in connected_components[1].nodes(data=True):
            j_coord = (j[1]['y'], j[1]['x'])
            dist = euclidean_dist_vec(i_coord[0], i_coord[1], j_coord[0], j_coord[1])
            if dist < closest_pair['dist']:
                closest_pair['i'] = i[0]
                closest_pair['j'] = j[0]
                closest_pair['dist'] = dist
    return closest_pair

The function takes a list of connected components, represented as NetworkX Graphs, and ordered by the size of the component. Then the main part of the algorithm is about finding the closest nodes between the two components.

Once that the missing link has been identified, the components can be connected. Following this approach and repeating it until all the components are connected into one single network can have a great impact in improving the bicycle connectivity in a city. Take the example from Budapest in the below video:

Just by investing in five new kilometers, the network gets from bellow 25% of their connections in one component to more than 50% 🤯. It is a great return of the investment.

When this algorithm was applied to different cities around the world[1], it highlighted the posibilites for improvement in the bicycle networks. This is a first approach to improve the connectivity in bicycle networks, extra measures are needed to ensure that the network is cohesive, resilient, and improves the directness of the paths in the network.

By using this type of algorithms, it is possible to have targeted urban interventions to improve the bicycle infrastructure in cities efficiently and economically. These algorithmic approaches are not only useful for planning and improving cities, it also allows simulations of interventions to provide insights into how urban mobility systems behaves after certain changes.

The combination of computer science, network science, and the urban environment is fascinating.

1. Natera Orozco Luis Guillermo, Battiston Federico, Iñiguez Gerardo and Szell Michael 2020 Data-driven strategies for optimal bicycle network growth R. Soc. open sci. 7:201130. 201130 http://doi.org/10.1098/rsos.201130